2D坐标系旋转平移总结
案例
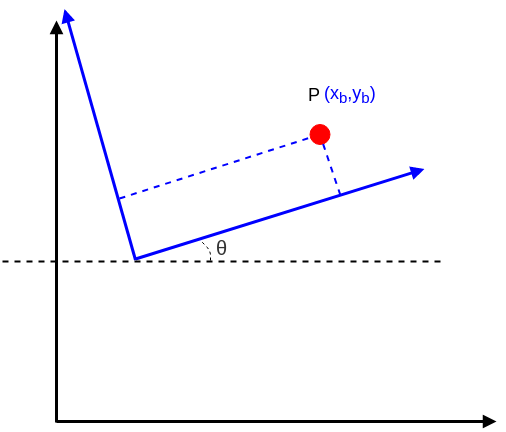
已知 红点在蓝色坐标系的位置(x_b, y_b),也知道蓝色坐标系相较于黑色坐标系 旋转的角度θ,
其中 蓝色坐标系的原点在黑色坐标系中的位置为(\delta x, \delta y).
求解: 红点在黑色坐标系同的位置(x_a, y_a)?
分析推导
黑色坐标系分析

在黑色坐标系中,我们为这个坐标系取名为A坐标系,红点为P,坐标系的原点取名为O_a。
我们要求解的是P点在A坐标系中的位置(x_a,y_a)。
其实P点在A坐标系中的位置(x_a,y_a),就是向量\vec {O_aP},表示为:
根据向量的特点,我们可以将\vec {O_aP} 分解为水平和垂直方向的两个向量\vec X和\vec Y:
\vec {O_aP}
=
\vec X
+
\vec Y
进一步,我们根据向量缩放的特点,可以定义水平和垂直方向的单位向量\vec {i_a} 和 \vec {j_a}, 那么:
\vec X = x_a \cdot \vec {i_a}
\vec Y = y_a \cdot \vec {j_a}
Note
x_a是x方向的数量,其实本质就是P点在A坐标系中的x坐标位置
y_a是y方向的数量,其实本质就是P点在A坐标系中的y坐标位置
总结以上,我们可以得到:
\vec {O_aP}
=
x_a \cdot \vec {i_a}
+
y_a \cdot \vec {j_a}
蓝色坐标系分析
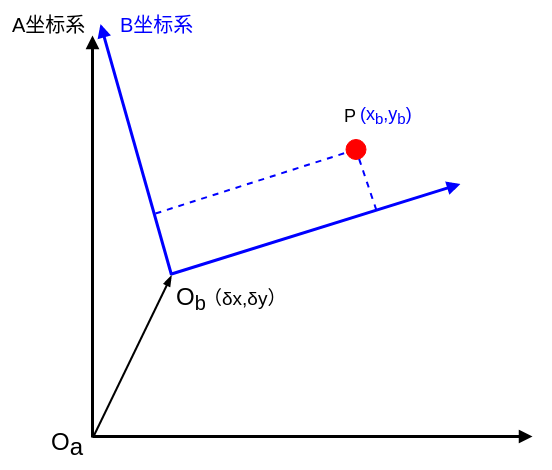
在黑色坐标系中,我们为这个坐标系取名为B坐标系,坐标系的原点取名为O_b。
已知的是O_b在A坐标系中的坐标位置为(\delta x, \delta y)。
其实O_b在A坐标系中的坐标位置(\delta x, \delta y) ,就是向量\vec {O_aO_b},表示为:
\vec {O_aO_b}
=
(\delta x, \delta y)
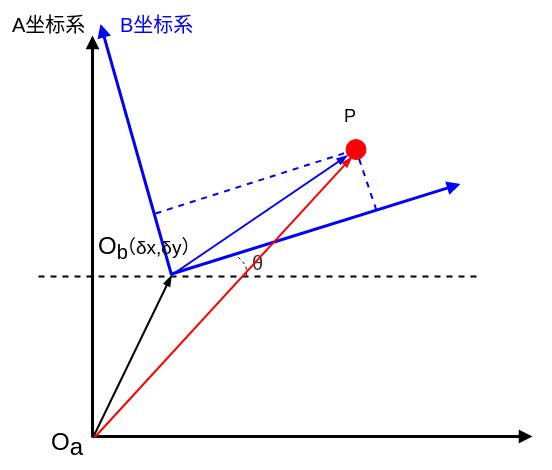
根据向量的三角形法则,我们可以知道:
\vec {O_aP}
=
\vec {O_aO_b}
+
\vec {O_bO_P}
向量\vec {O_aO_b} 和 向量\vec {O_aP}的坐标表示我们都是知道的,现在的问题是 如何表示向量\vec {O_bP}的坐标值。
在此处有个误区,大家可能会觉得\vec {O_bP} = (x_b, y_b)。
其实不是这样的,(x_b, y_b)坐标表示的是点P在B坐标系中的位置,视角是站在B坐标系上的,此时我们的视角应该是在A坐标系,或者是和A坐标系平行的。
那么,我们可以将B坐标系进行旋转,保证和A坐标系平行。

根据前面旋转部分的推导,我们可以得到:
\vec {O_bP}
=
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b
\end{matrix}
\right]
综合分析
已知:
(1)
\vec {O_aP}
=
\vec {O_aO_b}
+
\vec {O_bO_P}
(2)
(3)
\vec {O_aO_b}
=
(\delta x, \delta y)
(4)
\vec {O_bP}
=
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b
\end{matrix}
\right]
那么:
(x_a, y_a)
=
(\delta x, \delta y)
+
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b
\end{matrix}
\right]
正确的格式应该为:
\left[
\begin{matrix}
x_a \\
y_a
\end{matrix}
\right]
=
\left[
\begin{matrix}
\delta x \\
\delta y
\end{matrix}
\right]
+
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b
\end{matrix}
\right]
\left[
\begin{matrix}
x_a \\
y_a
\end{matrix}
\right]
=
\left[
\begin{matrix}
\delta x \\
\delta y
\end{matrix}
\right]
+
\left[
\begin{matrix}
cos(θ)*x_b - sin(θ)*y_b \\
sin(θ)*x_b + cos(θ)*y_b
\end{matrix}
\right]
\left[
\begin{matrix}
x_a \\
y_a
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(θ)*x_b - sin(θ)*y_b + \delta x\\
sin(θ)*x_b + cos(θ)*y_b + \delta y
\end{matrix}
\right]
转换成变换矩阵为:
\left[
\begin{matrix}
x_a \\
y_a \\
1
\end{matrix}
\right]
=
\left[
\begin{matrix}
cos(θ) & - sin(θ) & \delta x \\
sin(θ) & cos(θ) & \delta y \\
0 & 0 & 1
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b \\
1
\end{matrix}
\right]
总结
观察平移
前面我们总结过平移转换的矩阵:

其实我们将重点部分圈起来看:


观察旋转
总结过的旋转矩阵为:
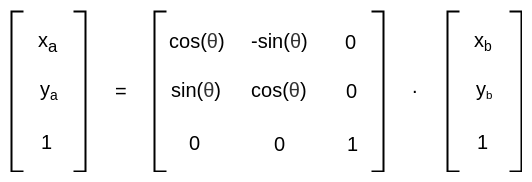
我们看看圈起来的部分:
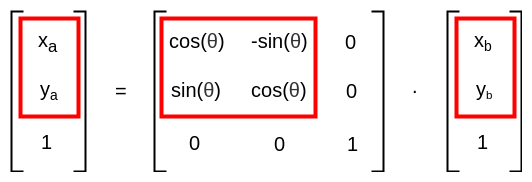

观察旋转和平移
总结的旋转和平移矩阵为:
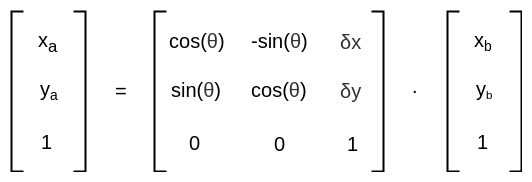
我们看看圈起来的部分:
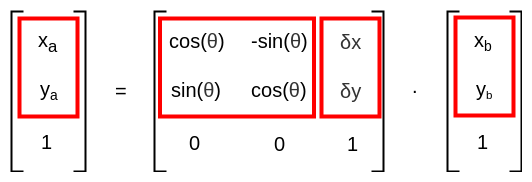

综合总结
在二维空间中,如果我们希望求解一个点在不同坐标间的转换,我们可以采用变换矩阵进行求解:
^A_BT
=
\left[
\begin{matrix}
cos(θ) & - sin(θ) & \delta x \\
sin(θ) & cos(θ) & \delta y \\
0 & 0 & 1
\end{matrix}
\right]
Note
T表示transform,变换的意思。
^A_BT 表示的是 由B坐标系变换为A坐标系的意思。
大致上我们可以得到以下:
P_b
=
^A_BT^{-1}
\cdot
P_a













