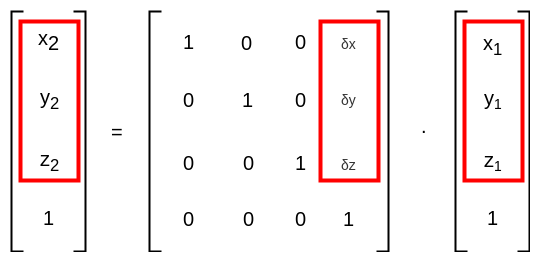
2D坐标系平移原理(向量)
案例¶

已知 红色点在蓝色坐标系的位置为(4, 1)
蓝色坐标系的原点在黑色坐标系中的位置为(2,3)
求解: 红色点在黑色坐标系中的位置点?
分析计算¶
蓝色坐标系¶
红色点在蓝色坐标系中的位置为(4,1),其实我们可以用向量的方式来看待:
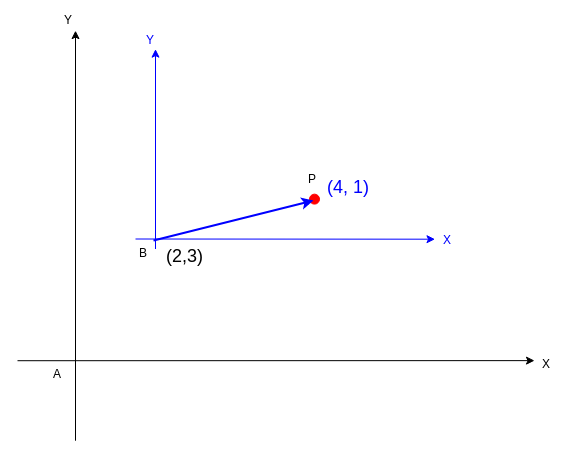
我们将蓝色坐标系的原点定义为B,将红色点定义为P。
红色点在蓝色坐标系的坐标点,我们可以看做是向量\vec {BP},那么: $$ \vec {BP} = (4, 1) $$
黑色坐标系¶
已知蓝色坐标系的原点B,在黑色坐标系中的位置(2, 3),我们用向量的方式看待:

我们将黑色坐标系的原点定义为A.
蓝色坐标系的原点B,我们可以看做是向量\vec {AB},那么:
\vec {AB} = (2, 3)
求解目标¶
我们要求解的是: 红色点在黑色坐标系中的位置点?
如果我们用向量方式思考,要求解的是\vec {AP}向量。
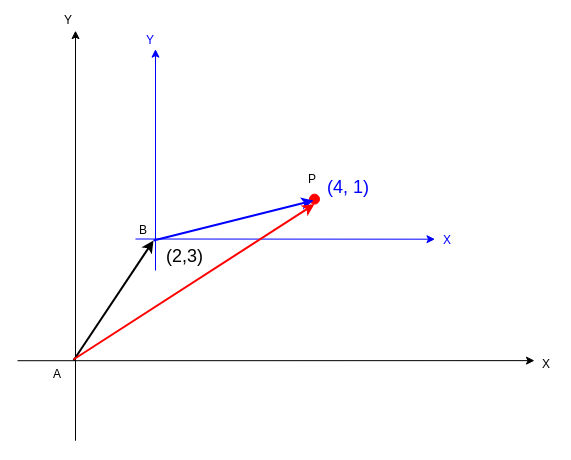
我们可以知道:
\vec {AP}
=
\vec {AB}
+
\vec {BP}
这里就回归到了向量的加法上来了,那么:
\vec {AP}
=
(2, 3)
+
(4, 1)
\vec {AP}
=
(6, 4)
分析抽象¶
由上面我们可以得到:
\vec {AP}
=
\vec {AB}
+
\vec {BP}
其中:
- \vec {AP} 的含义是,P点在黑色坐标系中的位置
- \vec {AB}的含义是,蓝色坐标系相对于黑色坐标系移动的位置
- \vec {BP}的含义是,P点在蓝色坐标系中的位置
我们分别进行抽象化:
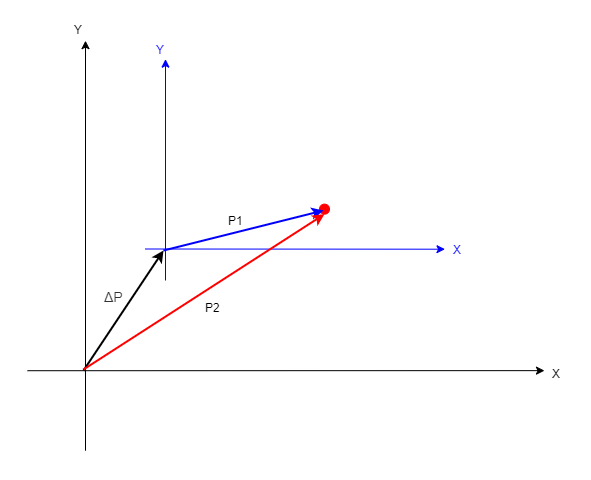
- \vec {P_1}向量表达的是点在蓝色坐标系中的位置
- \vec {P_2}向量表达的是点在黑色坐标系中的位置
- \vec {\Delta P}向量表达的是坐标平移的距离
那么:
\vec {P_2}
=
\vec {P_1}
+
\vec {\Delta P}
则:
(x_2, y_2) = (x_1, y_1) + (\delta x, \delta y)
\left\{
\begin{aligned}
x_2 = x_1 + \delta x \\
y_2 = y_1 + \delta y
\end{aligned}
\right.
\left\{
\begin{aligned}
x_2 = 1 * x_1 + 0 * y_1 + \delta x \\
y_2 = 0 * x_1 + 1 * y_1 + \delta y \\
1 = 0 * x_1 + 0 * y_1 + 1
\end{aligned}
\right.
则:
\left[\begin{matrix}
x_2 \\
y_2 \\
1
\end{matrix}
\right]
=
\left[\begin{matrix}
1 & 0 & \delta x \\
0 & 1 & \delta y \\
0 & 0 & 1
\end{matrix}
\right]
\cdot
\left[\begin{matrix}
x_1 \\
y_1 \\
1
\end{matrix}
\right]
公式总结¶
二维总结¶
根据以上推导我们可以得到以下的结论:
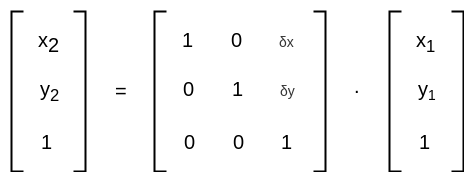
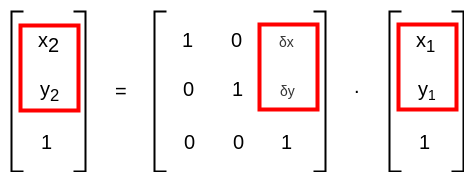

三维推导总结¶
\vec {P_2}
=
\vec {P_1}
+
\vec {\Delta F}
\left\{
\begin{aligned}
x_2 = x_1 + \delta x \\
y_2 = y_1 + \delta y \\
z_2 = z_1 + \delta z
\end{aligned}
\right.
\left\{
\begin{aligned}
x_2 = 1 * x_1 + 0 * y_1 + 0 * z_1 + \delta x \\
y_2 = 0 * x_1 + 1 * y_1 + 0 * z_1 + \delta y \\
z_2 = 0 * x_1 + 0 * y_1 + 1 * z_1 + \delta z \\
1 = 0 * x_1 + 0 * y_1 + 0 * z_1 + 1
\end{aligned}
\right.
\left[\begin{matrix}
x_2 \\
y_2 \\
z_2 \\
1
\end{matrix}
\right]
=
\left[\begin{matrix}
1 & 0 & 0 & \delta x \\
0 & 1 & 0 & \delta y \\
0 & 0 & 1 & \delta z \\
0 & 0 & 0 & 1
\end{matrix}
\right]
\cdot
\left[\begin{matrix}
x_1 \\
y_1 \\
z_1 \\
1
\end{matrix}
\right]