2D坐标系旋转原理
案例
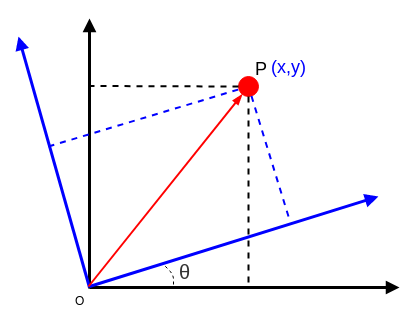
已知 红点在蓝色坐标系的位置(x, y),也知道蓝色坐标系相较于黑色坐标系旋转的角度θ。
求解: 红点在黑色坐标系同的位置(dstX, dstY)?
推导分析
黑色坐标系分析

在黑色坐标系中(A坐标系),我们用向量的方式来进行分析。
首先,我们可以把 \vec {OP} 可以分解为 水平坐标方向的两个向量:
\vec {OP}
=
\vec {X_a}
+
\vec {Y_a}
根据向量的缩放特性,我们定义一个x轴方向的 单位向量\vec {i_a},方向沿着x轴,模长为1.
我们定义一个y轴方向的 单位向量\vec {j_a},方向沿y轴,模长为1.
那么:
\vec {X_a} = x_a \cdot \vec {i_a}
\vec {Y_a} = y_a \cdot \vec {j_a}
Note
x_a是x方向的数量,其实本质就是p点在A坐标系中的x坐标位置
y_a是y方向的数量,其实本质就是p点在A坐标系中的y坐标位置
总的来说,我们可以得到以下结果:
\vec {OP} = x_a \cdot \vec {i_a} + y_a \cdot \vec {j_a}
蓝色坐标系分析
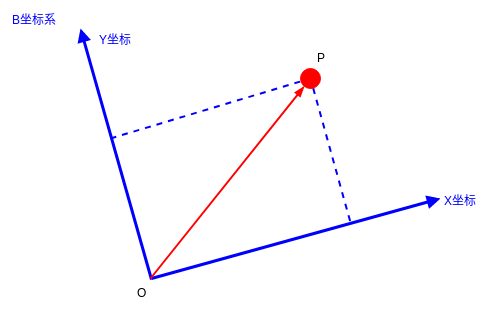
在蓝色坐标系中(B坐标系),我们用向量的方式来进行分析。
首先,我们可以把 \vec {OP} 可以分解为 水平坐标方向的两个向量:
\vec {OP}
=
\vec {X_b}
+
\vec {Y_b}
根据向量的缩放特性,我们定义一个x轴方向的 单位向量 \vec {i_b},方向沿着x轴,模长为1.
我们定义一个y轴方向的 单位向量\vec {j_b},方向沿y轴,模长为1.
那么:
\vec {X_b} = x_b \cdot \vec {i_b}
\vec {Y_b} = y_b \cdot \vec {j_b}
Note
x_b是x方向的数量,其实本质就是p点在B坐标系中的x坐标位置
y_b是y方向的数量,其实本质就是p点在B坐标系中的y坐标位置
总的来说,我们可以得到以下结果:
\vec {OP} = x_b \cdot \vec {i_b} + y_b \cdot \vec {j_b}
整体分析
对于向量\vec {OP}而言,无论在A坐标系还是B坐标系,他的方向和模长是没有变的,只是观测者不同。
我们根据以上的分析,基本上可以得到:
\vec {OP} = x_a \cdot \vec {i_a} + y_a \cdot \vec {j_a}
\vec {OP} = x_b \cdot \vec {i_b} + y_b \cdot \vec {j_b}
那么:
x_a \cdot \vec {i_a} + y_a \cdot \vec {j_a}
=
x_b \cdot \vec {i_b} + y_b \cdot \vec {j_b}
推导过程-1
我们将式子的两边同时点乘一个\vec {i_a}
x_a \cdot \vec {i_a} \cdot \vec {i_a}
+
y_a \cdot \vec {j_a} \cdot \vec {i_a}
=
x_b \cdot \vec {i_b} \cdot \vec {i_a}
+
y_b \cdot \vec {j_b} \cdot \vec {i_a}
在左边的式子中:
\vec {i_a} * \vec {i_a} = 1
\vec {j_a} \cdot \vec {i_a} = 0
Tip
两个单位向量点乘,他们的夹角为0时,结果为1.
两个单位向量点乘,他们的夹角为90时,结果为0.
那么左边的式子化简结果为:
x_a \cdot 1
+
y_a \cdot 0
=
x_b \cdot \vec {i_b} \cdot \vec {i_a}
+
y_b \cdot \vec {j_b} \cdot \vec {i_a}
结果为:
x_a
=
x_b \cdot \vec {i_b} \cdot \vec {i_a}
+
y_b \cdot \vec {j_b} \cdot \vec {i_a}
推导过程-2
我们将式子的两边同时点乘一个\vec {j_a}
x_a \cdot \vec {i_a} \cdot \vec {j_a}
+
y_a \cdot \vec {j_a} \cdot \vec {j_a}
=
x_b \cdot \vec {i_b} \cdot \vec {j_a}
+
y_b \cdot \vec {j_b} \cdot \vec {j_a}
在左边的式子中:
\vec {i_a} * \vec {j_a} = 0
\vec {j_a} \cdot \vec {j_a} = 1
Tip
两个单位向量点乘,他们的夹角为0时,结果为1.
两个单位向量点乘,他们的夹角为90时,结果为0.
那么左边的式子化简结果为:
x_a \cdot 0
+
y_a \cdot 1
=
x_b \cdot \vec {i_b} \cdot \vec {j_a}
+
y_b \cdot \vec {j_b} \cdot \vec {j_a}
结果为:
y_a
=
x_b \cdot \vec {i_b} \cdot \vec {j_a}
+
y_b \cdot \vec {j_b} \cdot \vec {j_a}
整理推导
以上可以得到:
x_a
=
x_b \cdot \vec {i_b} \cdot \vec {i_a}
+
y_b \cdot \vec {j_b} \cdot \vec {i_a}
y_a
=
x_b \cdot \vec {i_b} \cdot \vec {j_a}
+
y_b \cdot \vec {j_b} \cdot \vec {j_a}
在这里,x_a和y_a是 点P在黑色坐标系(A坐标系)中的坐标点位置 ,是 未知的,是需要我们计算出来的。
x_b和y_b是 点P在蓝色坐标系(B坐标系)中的坐标点位置,是 已知的。
我们将以上式子化简为 矩阵运算 的结果:
\left[
\begin{matrix}
\vec {i_b} \cdot \vec {i_a} & \vec {j_b} \cdot \vec {i_a} \\
\vec {i_b} \cdot \vec {j_a} & \vec {j_b} \cdot \vec {j_a} \\
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
x_a \\
y_a \\
\end{matrix}
\right]
我们继续推导,来看看:
(1):
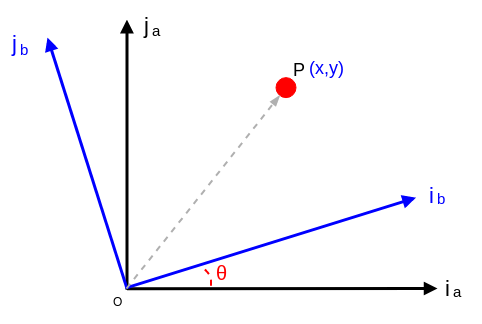
单位向量i_b和i_a之间的夹角为θ,因此
\vec {i_b} \cdot \vec {i_a}
=
|\vec {i_b}| \cdot |\vec {i_a}| \cdot cos(θ)
\vec {i_b} \cdot \vec {i_a}
=
1 \cdot 1 \cdot cos(θ)
\vec {i_b} \cdot \vec {i_a} = cos(θ)
(2):
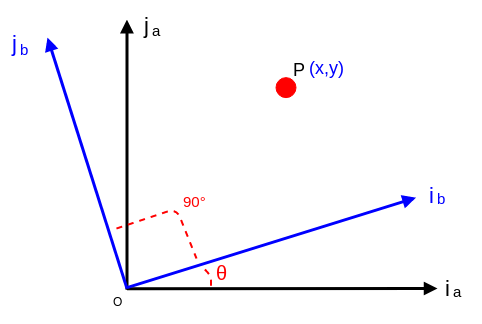
单位向量i_b和i_a之间的夹角为(90 + θ),因此
\vec {j_b} \cdot \vec {i_a}
=
|\vec {i_b}| \cdot |\vec {i_a}| \cdot cos(90 + θ)
\vec {j_b} \cdot \vec {i_a}
=
1 \cdot 1 \cdot -sin(θ)
\vec {j_b} \cdot \vec {i_a}
=
-sin(θ)
(3):
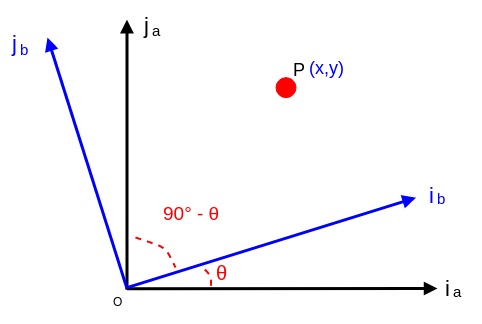
单位向量 i_b 和 j_a 之间的夹角为(90 - θ),因此
\vec {i_b} \cdot \vec {j_a}
=
|\vec {i_b}| \cdot |\vec {j_a}| \cdot cos(90 - θ)
\vec {i_b} \cdot \vec {j_a}
=
1 \cdot 1 \cdot sin(θ)
\vec {i_b} \cdot \vec {j_a}
=
sin(θ)
(4):
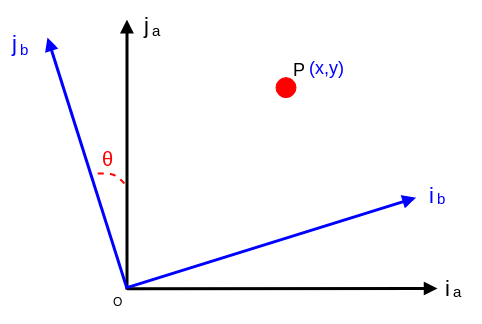
单位向量 j_b 和 j_a 之间的夹角为θ,因此
\vec {j_b} \cdot \vec {j_a}
=
|\vec {j_b}| \cdot |\vec {j_a}| \cdot cos(θ)
\vec {j_b} \cdot \vec {j_a}
=
1 \cdot 1 \cdot cos(θ)
\vec {j_b} \cdot \vec {j_a}
=
cos(θ)
根据以上推动结果,我们可以得到一个完整的矩阵式子:
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
x_a \\
y_a \\
\end{matrix}
\right]
总结
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
\cdot
\left[
\begin{matrix}
x_b \\
y_b \\
\end{matrix}
\right]
=
\left[
\begin{matrix}
x_a \\
y_a \\
\end{matrix}
\right]






